Intro
Master the art of vector calculations with our step-by-step guide on how to calculate cross product. Learn the 5 easy steps to find the cross product of two vectors, including understanding vector components, using the right-hand rule, and applying the formula. Improve your math skills and boost your understanding of physics and engineering concepts.
The cross product, also known as the vector product, is a fundamental concept in mathematics and physics that is used to describe the interaction between two vectors in three-dimensional space. Calculating the cross product can be a challenging task, but with the right approach, it can be done with ease. In this article, we will provide a step-by-step guide on how to calculate the cross product of two vectors.
What is the Cross Product?
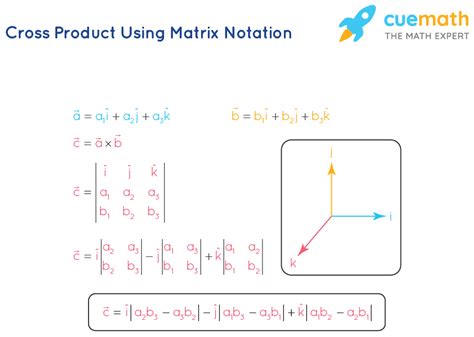
The cross product is a binary operation that takes two vectors in three-dimensional space and returns another vector that is perpendicular to both of the original vectors. The resulting vector is also known as the normal vector. The cross product is denoted by the symbol × and is calculated using the following formula:
a × b = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
where a = (a1, a2, a3) and b = (b1, b2, b3) are two vectors in three-dimensional space.
Step 1: Identify the Vectors

The first step in calculating the cross product is to identify the two vectors that you want to calculate the cross product of. These vectors should be in three-dimensional space and should be represented in the form (x, y, z).
Example:
Let's say we have two vectors a = (1, 2, 3) and b = (4, 5, 6). We want to calculate the cross product of these two vectors.
Step 2: Calculate the Components

Once we have identified the vectors, the next step is to calculate the components of the cross product. This involves multiplying the corresponding components of the two vectors and then subtracting the products.
Using the formula above, we can calculate the components of the cross product as follows:
a2b3 - a3b2 = 2(6) - 3(5) = 12 - 15 = -3 a3b1 - a1b3 = 3(4) - 1(6) = 12 - 6 = 6 a1b2 - a2b1 = 1(5) - 2(4) = 5 - 8 = -3
Step 3: Write the Resulting Vector

Now that we have calculated the components of the cross product, we can write the resulting vector. The resulting vector is a vector that is perpendicular to both of the original vectors.
Using the components that we calculated above, we can write the resulting vector as:
(-3, 6, -3)
Step 4: Check the Result

Once we have calculated the cross product, it's always a good idea to check the result. We can do this by calculating the dot product of the resulting vector and one of the original vectors. If the resulting vector is perpendicular to the original vector, then the dot product should be zero.
Using the formula for the dot product, we can calculate the dot product of the resulting vector and one of the original vectors as follows:
(-3, 6, -3) · (1, 2, 3) = -3(1) + 6(2) + (-3)(3) = -3 + 12 - 9 = 0
Since the dot product is zero, we can confirm that the resulting vector is perpendicular to the original vector.
Step 5: Interpret the Result

Finally, we need to interpret the result. The resulting vector is a vector that is perpendicular to both of the original vectors. This vector can be used to describe the interaction between the two original vectors.
In our example, the resulting vector (-3, 6, -3) can be used to describe the interaction between the two vectors a = (1, 2, 3) and b = (4, 5, 6).
By following these 5 easy steps, you can calculate the cross product of two vectors with ease. Remember to identify the vectors, calculate the components, write the resulting vector, check the result, and interpret the result.
What is the cross product used for?
+The cross product is used to describe the interaction between two vectors in three-dimensional space. It is used in physics, engineering, and computer science to calculate the normal vector to a surface, the torque of a force, and the area of a parallelogram.
How do I calculate the cross product of two vectors?
+To calculate the cross product of two vectors, you need to follow these 5 easy steps: identify the vectors, calculate the components, write the resulting vector, check the result, and interpret the result.
What is the resulting vector of the cross product?
+The resulting vector of the cross product is a vector that is perpendicular to both of the original vectors. It can be used to describe the interaction between the two original vectors.
We hope this article has helped you to understand how to calculate the cross product of two vectors. If you have any questions or need further clarification, please don't hesitate to ask.
