Find The Radius Of A Circle With Ease

Circles are a fundamental concept in mathematics and geometry, and understanding their properties is essential for various mathematical and real-world applications. One of the most important properties of a circle is its radius, which is the distance from the center of the circle to any point on its circumference. In this article, we will explore the concept of the radius of a circle, its importance, and various methods to find it.

Understanding the Radius of a Circle

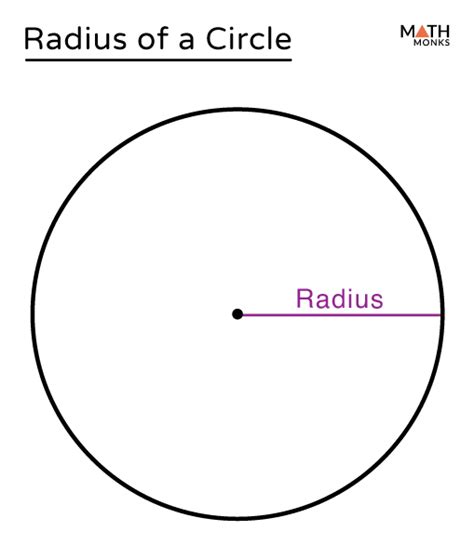
The radius of a circle is a line segment that connects the center of the circle to any point on its circumference. It is half the length of the diameter, which is the distance across the circle passing through its center. The radius is an essential concept in geometry, trigonometry, and mathematics, and it has numerous applications in physics, engineering, and other fields.

Importance of the Radius of a Circle

The radius of a circle is crucial in various mathematical and real-world applications. Some of the reasons why the radius is important include:

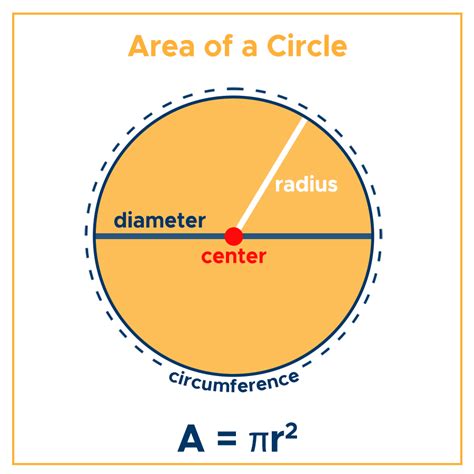
Area and circumference calculation: The radius is used to calculate the area and circumference of a circle. The area of a circle is given by the formula A = πr^2, where A is the area and r is the radius. The circumference of a circle is given by the formula C = 2πr, where C is the circumference and r is the radius.
Circle properties: The radius is used to define various properties of a circle, such as its center, diameter, and circumference.
Geometry and trigonometry: The radius is used in geometry and trigonometry to calculate distances, angles, and shapes.
Physics and engineering: The radius is used in physics and engineering to calculate forces, velocities, and energies.

Methods to Find the Radius of a Circle

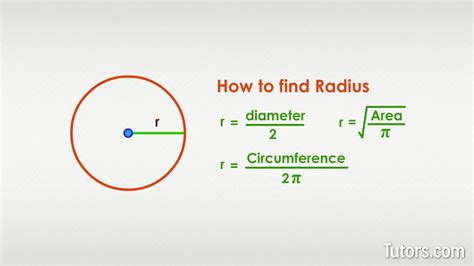
There are several methods to find the radius of a circle, depending on the given information. Some of the common methods include:

Using the diameter: If the diameter of the circle is given, the radius can be found by dividing the diameter by 2.
Using the circumference: If the circumference of the circle is given, the radius can be found by dividing the circumference by 2π.
Using the area: If the area of the circle is given, the radius can be found by taking the square root of the area divided by π.
Using the chord and arc: If the length of a chord and the corresponding arc are given, the radius can be found using the formula r = (c^2 + 4a^2) / (8a), where c is the length of the chord and a is the length of the arc.

Step-by-Step Guide to Finding the Radius of a Circle

Here is a step-by-step guide to finding the radius of a circle:

Identify the given information: Identify the given information, such as the diameter, circumference, area, or chord and arc.
Choose the relevant formula: Choose the relevant formula to find the radius, depending on the given information.
Plug in the values: Plug in the values into the formula and simplify.
Solve for the radius: Solve for the radius and express it in the simplest form.

Real-World Applications of the Radius of a Circle

The radius of a circle has numerous real-world applications, including:

Architecture: The radius is used in architecture to design circular structures, such as domes, arches, and columns.
Engineering: The radius is used in engineering to design circular systems, such as pipes, tubes, and gears.
Physics: The radius is used in physics to calculate forces, velocities, and energies.
Computer graphics: The radius is used in computer graphics to create circular shapes and objects.

Conclusion

In conclusion, the radius of a circle is a fundamental concept in mathematics and geometry, and it has numerous applications in various fields. Understanding the radius of a circle is essential for solving problems and designing systems in physics, engineering, architecture, and computer graphics. By using the formulas and methods outlined in this article, you can easily find the radius of a circle and apply it to real-world problems.

What is the definition of the radius of a circle?

The radius of a circle is the distance from the center of the circle to any point on its circumference.

How do I find the radius of a circle if the diameter is given?

If the diameter is given, the radius can be found by dividing the diameter by 2.

What are some real-world applications of the radius of a circle?

The radius of a circle has numerous real-world applications, including architecture, engineering, physics, and computer graphics.

We hope this article has helped you understand the concept of the radius of a circle and its importance in various fields. If you have any questions or comments, please feel free to share them below.