Intro
Discover the simplicity of finding roots with our easy-to-follow guide. Learn 3 straightforward methods to calculate the root of any number, covering basic arithmetic operations, algebraic manipulations, and clever tricks. Master square roots, cube roots, and more with our step-by-step explanations and examples, perfect for math students and enthusiasts alike.
Finding the root of a number, whether it's a square root, cube root, or any other root, is a fundamental concept in mathematics. It's a crucial operation in various mathematical calculations, from simple arithmetic to advanced algebra and calculus. However, for many, especially those who struggle with math or haven't practiced in a while, finding roots can be daunting. Fortunately, there are straightforward methods to find the root of any number, and we'll explore three easy ways to do so.
Mathematics is all about solving problems, and understanding how to find roots is a key part of that. Whether you're a student looking to improve your math skills, a professional needing to brush up on old concepts, or simply someone curious about numbers, knowing how to find roots efficiently can make a big difference. In this article, we'll break down three easy methods to find the root of any number, making math more accessible and enjoyable for everyone.

Understanding Roots
Before we dive into the methods, it's essential to understand what roots are. In mathematics, a root of a number is a value that, when raised to a power (the root), gives the original number. For example, the square root of 16 is 4 because 4^2 = 16. Similarly, the cube root of 27 is 3 because 3^3 = 27.
Types of Roots
- Square Root: The square root of a number is a value that, when multiplied by itself, gives the original number. It's denoted by √.
- Cube Root: The cube root of a number is a value that, when cubed, gives the original number. It's denoted by ³√.
- Nth Root: This is a general term for any root, where 'n' represents the power to which the root is raised.
Method 1: Using a Calculator

One of the easiest and most straightforward ways to find the root of a number is by using a calculator. Most calculators, even basic ones, have functions for square roots and sometimes cube roots. For nth roots, you might need a scientific calculator.
- Steps for Using a Calculator:
- Enter the number for which you want to find the root.
- Press the root function button (√ for square root, or ³√ for cube root).
- If using a scientific calculator for an nth root, enter the number, press the "x^y" button, enter the root value as the exponent, and calculate.
Method 2: Estimation and Long Division
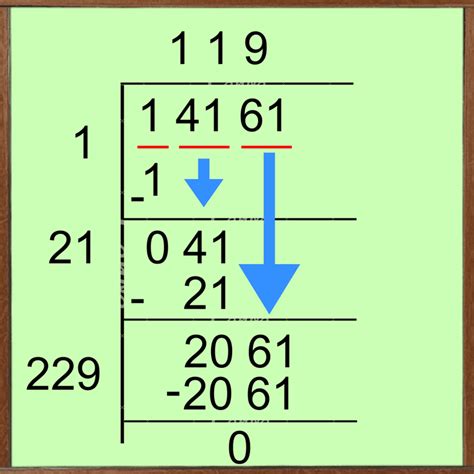
For those without a calculator, or as a way to understand the process better, you can use estimation and long division to find roots. This method is particularly useful for square roots.
- Steps for Estimation and Long Division:
- Estimate the root: Start by guessing a number that, when squared (or cubed, etc.), might give you the original number.
- Divide the number by your guess: Use long division to divide the original number by your estimated root.
- Refine your guess: Based on the quotient, adjust your guess and repeat the division process until you get a more accurate root.
Method 3: Using Algebraic Formulas

For a more precise approach, especially in mathematical derivations, using algebraic formulas can be very effective. However, this method requires a good understanding of algebraic manipulations.
- Steps for Using Algebraic Formulas:
- Express the number as an algebraic expression: If possible, express the number for which you want to find the root in terms of algebraic expressions that can be easily manipulated.
- Apply algebraic manipulations: Use algebraic rules to isolate the variable representing the root.
- Solve for the root: Once isolated, solve for the value of the root.
Conclusion and Next Steps
Finding the root of a number doesn't have to be a daunting task. Whether you use a calculator for quick solutions, estimation and long division for a more manual approach, or algebraic formulas for precision, understanding roots is a fundamental part of mathematics that can open doors to more complex and fascinating concepts.
By practicing these methods, you'll not only become more proficient in finding roots but also develop a deeper appreciation for the underlying mathematics. So, next time you encounter a problem requiring you to find a root, remember these three easy methods and make math a little more enjoyable.

Share Your Thoughts
Finding roots is a fundamental math concept, but everyone learns differently. Share with us your favorite method for finding roots, or ask a question if you're still unsure. Let's make math more accessible together!
What is the difference between a square root and a cube root?
+A square root of a number is a value that, when multiplied by itself, gives the original number. A cube root of a number is a value that, when cubed, gives the original number.
How do I find the nth root of a number without a calculator?
+You can use estimation and long division, or algebraic formulas. The method you choose will depend on your comfort level with algebra and the specific problem you're trying to solve.
Why is finding roots important in mathematics?
+Finding roots is crucial in various mathematical calculations, from solving quadratic equations to more complex problems in algebra and calculus. It's a fundamental concept that helps in understanding and solving a wide range of mathematical problems.
