Domain And Range: Understanding The Basics Of Functions

In the realm of mathematics, functions play a crucial role in describing relationships between variables. Two fundamental concepts in understanding functions are domain and range. These concepts are essential in mathematics, science, and engineering, as they help us analyze and interpret the behavior of functions. In this article, we will delve into the world of domain and range, exploring their definitions, importance, and applications.

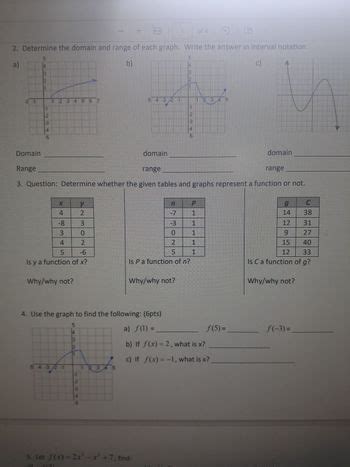
What is Domain?

The domain of a function is the set of all possible input values for which the function is defined. In other words, it is the set of all values that can be plugged into the function without resulting in an undefined or imaginary output. The domain is typically represented by the variable x and is often denoted as the set of real numbers, R.

For example, consider the function f(x) = 1/x. The domain of this function is all real numbers except x = 0, since dividing by zero is undefined. Therefore, the domain of f(x) = 1/x is (-∞, 0) ∪ (0, ∞).

Types of Domain

There are several types of domain, including:

Finite domain: A domain that contains a finite number of elements.
Infinite domain: A domain that contains an infinite number of elements.
Discrete domain: A domain that consists of distinct, isolated points.
Continuous domain: A domain that consists of all real numbers within a certain interval.

What is Range?

The range of a function is the set of all possible output values it can produce. In other words, it is the set of all values that the function can take on. The range is typically represented by the variable y and is often denoted as the set of real numbers, R.

For example, consider the function f(x) = x^2. The range of this function is all non-negative real numbers, since the square of any real number is always non-negative. Therefore, the range of f(x) = x^2 is [0, ∞).

Types of Range

There are several types of range, including:

Finite range: A range that contains a finite number of elements.
Infinite range: A range that contains an infinite number of elements.
Discrete range: A range that consists of distinct, isolated points.
Continuous range: A range that consists of all real numbers within a certain interval.

Importance of Domain and Range

Understanding the domain and range of a function is crucial in various fields, including:

Mathematics: Domain and range help us analyze and interpret the behavior of functions, which is essential in calculus, algebra, and geometry.
Science: Domain and range are used to model real-world phenomena, such as the motion of objects, population growth, and chemical reactions.
Engineering: Domain and range are used to design and optimize systems, such as electronic circuits, mechanical systems, and computer networks.

Real-World Applications

Domain and range have numerous real-world applications, including:

Predicting stock prices: Domain and range can be used to model the behavior of stock prices, helping investors make informed decisions.
Optimizing traffic flow: Domain and range can be used to model traffic flow, helping urban planners design more efficient transportation systems.
Modeling population growth: Domain and range can be used to model population growth, helping demographers predict future population trends.

How to Find Domain and Range

Finding the domain and range of a function can be done using various techniques, including:

Graphical method: Plotting the function on a graph and identifying the x-values for which the function is defined.
Algebraic method: Analyzing the function's equation and identifying the x-values for which the function is defined.
Numerical method: Using numerical methods, such as the bisection method, to approximate the domain and range of a function.

Common Mistakes

When finding the domain and range of a function, common mistakes include:

Ignoring restrictions: Failing to account for restrictions on the domain, such as dividing by zero.
Misidentifying the range: Failing to identify the correct range of a function, such as mistaking the range for the domain.

Conclusion

In conclusion, domain and range are fundamental concepts in understanding functions. They help us analyze and interpret the behavior of functions, which is essential in various fields, including mathematics, science, and engineering. By understanding domain and range, we can make informed decisions, optimize systems, and model real-world phenomena.

We hope this article has provided you with a comprehensive understanding of domain and range. If you have any questions or comments, please feel free to share them below.

What is the difference between domain and range?

The domain is the set of all possible input values for which the function is defined, while the range is the set of all possible output values the function can produce.

How do I find the domain of a function?

You can find the domain of a function by using the graphical method, algebraic method, or numerical method.

What is the importance of domain and range in real-world applications?

Domain and range are used to model real-world phenomena, such as population growth, traffic flow, and stock prices, helping us make informed decisions and optimize systems.